Definition of Graphs
A graph is a pair of sets, \((V, E)\) where \(E \subset V \times V.\)
The set \(V\) is called the vertext set and the set \(E\) is call the edge set. An element of \(V\) is called a vertex and an element of \(E\) is called an edge.
An undirected graph satisfies the following condition:
If \((i,j) \in E\) then \((j,i) \in E.\)
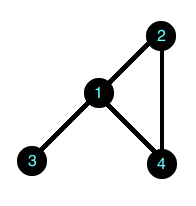
For example, an undirected graph \(G\) can have a vertex set \(V = \{1, 2, 3, 4\}\) and an edge set \(E = \{(1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (2, 4), (4, 2)\}.\)
Usually the data is hard to read but it can be a useful representation when writing a proof. It is more common to represent a graph with a picture.
To draw the picture, first draw a point for each vertex. In this picture, the vertices are labeled with their names, \(V = \{1, 2, 3, 4\}.\)
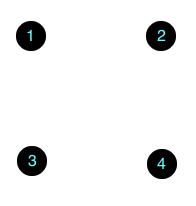
Next, for each edge \((i, j) \in E,\) draw a line between vertices \(i\) and \(j.\) For example, since \((1, 3) \in E,\) there is a line beween vertices \(1\) and \(3.\)
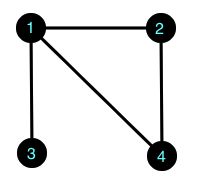
The connections represent the elements of the edge set
\[E = \{(1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (2, 4), (4, 2)\}\]